INNOVATING NEW SOLUTIONS
Mission Statement
Perform leading edge basic and applied research in electrical and mechanical engineering, with a special emphasis on applied engineering leading to prototype development in electromechanical devices and systems with high specific power, force, and/or energy storage or other unique attributes. Imbedded in this mission is educating and developing students and CEM staff members into engineering leaders of tomorrow.
Vision Statement
For CEM to be internationally renowned in its mission area.
For CEM’s people to be internationally renowned in their areas of expertise.
LATEST NEWS

UT and U.S. Army Researchers Replicate Real-life Tech Lab for Summer Camp Students
Hosted by UT-CEM and ARL South, the Gains in Education of Mathematics and Science (GEMS) camp has been featured in a UT Campus & Community article.

KCEN TV Features CEM's Bob Hebner
On Monday, August 7, 2023, KCEN TV in Temple, TX featured CEM's Bob Hebner in a story about the Texas Power Grid.

The Hydrogen Podcast Interview Featuring Mike Lewis
Hydrogen Podcast episode which features CEM’s Mike Lewis. The podcast discusses several of CEM’s H2 activities, as well as the DOE H2 Scale project.

Hydrogen energy may be on the cusp. And Texas has potential to lead
Researchers at UT-Austin developed a hydrogen refueling station for use in larger projects testing hydrogen energy in vehicles.
Story by: Diego Mendoza-Moyers
Conferences and Events
No conferences or events at this time
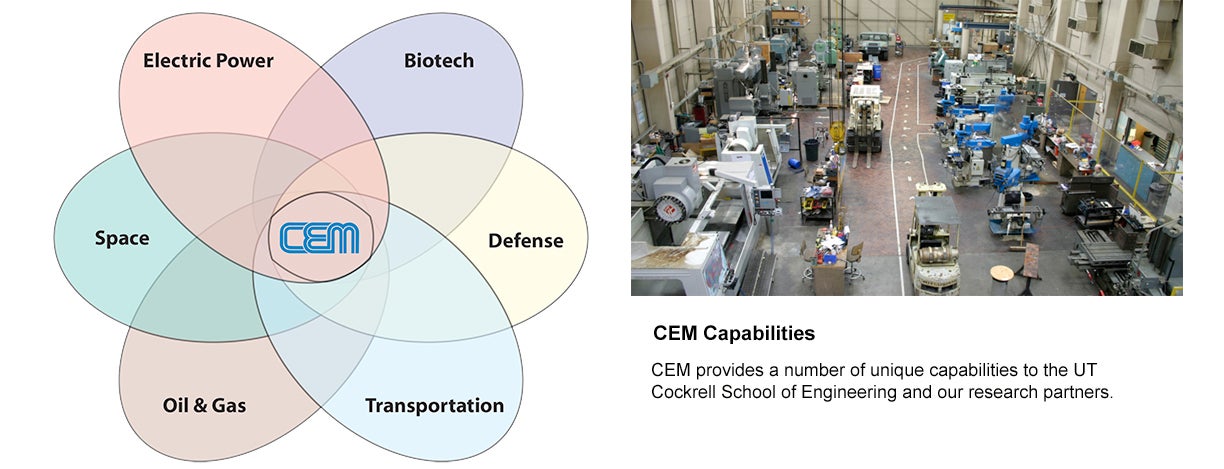
Our approach involves participation in a continuum of research projects, each contributing to our knowledge base and core competencies while leveraging the results and experiences gained in previous projects. We intend to always be on the forefront of the new age of electrification by applying our fundamental understanding of the technologies involved to an increasing number of novel application areas.
CENTER FOR ELECTROMECHANICS
- Location:
-
10500 Exploration Way
Austin, Texas 78758
- Address:
-
The Center for Electromechanics
10500 Exploration Way
Austin, TX 78758
- Phone:
- Fax:
-
512-471-0781
- Website:

